B-Arbre
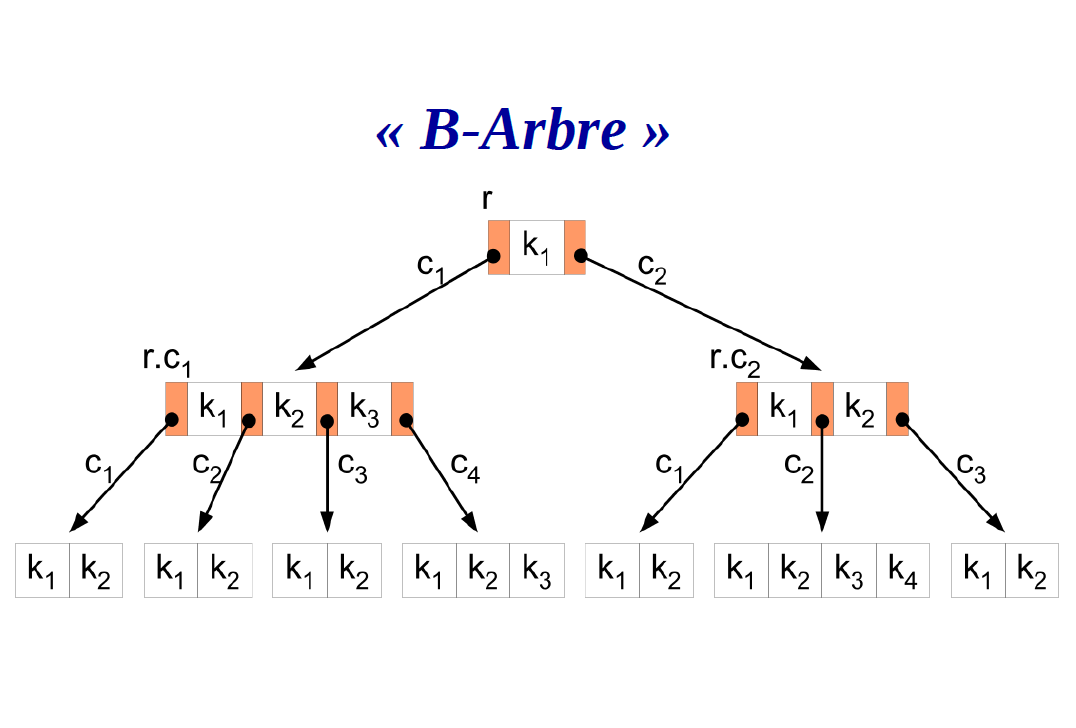
B-arbre (ou B-tree, en Anglais) Est structures de données/ méthodes qui permettent la localisation rapide du fichier (archives ou des clés), en particulier dans base de données, réduire le nombre de fois qu'un utilisateur a besoin d'accéder à la mémoire où les données sont enregistrées.
B-Tree est connu comme un arbre auto-équilibré car ses nodes sont triés dans le parcours inorder.
Dans B-tree, un node peut avoir plus de deux enfants. B-tree a une hauteur de logM N (Où ‘M’ est l’ordre de l’arbre et N est le nombre de nodes). Et la hauteur est ajustée automatiquement à chaque mise à jour.
Dans l’arbre B, les données sont triées dans un ordre spécifique, avec la valeur la plus basse à gauche et la valeur la plus élevée à droite. Insérer la donnée ou la clé dans un arbre B est plus compliqué qu’un arbre binaire. Certaines conditions doivent être tenues par le B-Tree :
- Tous les nodes feuilles du B-tree doivent être au même niveau.
- Au-dessus des nodes feuilles du B-tree, il ne devrait y avoir aucun sous-arbre vide.
- La hauteur de l’arbre B doit être aussi basse que possible.
Implémentation d'un B-arbre en JAVA :
Le degré minimal de notre B-arbre égale à 3, et il faut faire le stockage de 10000 entiers choisies aléatoirement (10000 < x < 99999).
- Définition de deux classes Nœud et Couple
import java.util.ArrayList;
class Noeud {
boolean feuille; // true si le noeud est une feuille
int n; // nombre de cle dans le noeud
int[] cle; // tableau des cles du noeud
Noeud[] c; // tableau des pointeurs sur les fils
Noeud(int t){
this.cle = new int[2*t-1];
this.c = new Noeud[2*t];
this.n = 0;
this.feuille = true;
}
/* fonction pour afficher la liste des noeuds du Barbre */
public void afficherListe(){
int i;
for(i=0;i<=this.n;i++){
if(!this.feuille){
if(this.c[i]!=null){
this.c[i].afficherListe();
}
}
if(i<this.n) {
System.out.print(this.cle[i]+"|");
}
}
}
}
class Couple{
Noeud x;
int i;
Couple(Noeud a, int b){
this.x=a;
this.i=b;
}
Couple(){}
}
- Class Barbre et la fonction Main
import java.util.ArrayList;
import java.util.Scanner;
class Barbre {
Noeud racine;
final int t=3;
/* construction du Barbre */
Barbre(){
Noeud r = new Noeud(this.t);
this.racine = r;
}
/* recherche d'un element dans le Barbre */
public Couple rechercher(int k){
return this.rechercherBis(this.racine,k);
}
public Couple rechercherBis(Noeud x,int k){
int i =0;
while(i<x.n && k>x.cle[i]){
i++;
}
if(i<x.n && k==x.cle[i]){
return new Couple(x,i);
}
if(x.feuille)
return null;
else
return rechercherBis(x.c[i],k);
}
/* Insertion d'un element dans le Barbre*/
public void inserer(int k){
Noeud r = this.racine;
if(r.n == 2*t-1){
Noeud s = new Noeud(3);
this.racine=s;
s.feuille=false;
s.n=0;
s.c[0]=r;
this.decouperFils(s,0,r);
this.insererBArbreIncomplet(s,k);
}else{
this.insererBArbreIncomplet(r,k);
}
}
public void insererBArbreIncomplet(Noeud x, int k){
int i=x.n;
if(x.feuille){
while(i>=1 && k<x.cle[i-1]){
x.cle[i]=x.cle[i-1];
i--;
}
x.cle[i]=k;
x.n++;
}else{
while(i>=1 && k<x.cle[i-1]){
i--;
}
if(x.c[i]==null)
x.c[i] = new Noeud(this.t);
if(x.c[i].n==2*t-1){
decouperFils(x,i,x.c[i]);
if(k>x.cle[i])
i++;
}
insererBArbreIncomplet(x.c[i],k);
}
}
public void decouperFils(Noeud x,int i, Noeud y){
Noeud z=new Noeud(this.t);
int j;
z.n=this.t-1;
z.feuille=y.feuille;
for(j=0;j<this.t-1;j++){
z.cle[j]=y.cle[j+this.t];
}
if(!z.feuille){
for(j=0;j<this.t;j++){
z.c[j]=y.c[j+this.t];
}
}
y.n=this.t-1;
for(j=x.n+1;j<=i+1;j++){
x.c[j]=x.c[j-1];
}
x.c[i+1]=z;
for(j=x.n-1;j>=i;j--){
x.cle[j+1]=x.cle[j];
}
x.cle[i]=y.cle[this.t-1];
x.n++;
}
public void afficherArbreListe(){
this.racine.afficherListe();
System.out.println();
}
/* fonction main */
public static void main(String args[]){
Barbre arbre = new Barbre();
int i,r, n;
for(i=1;i<1000;i++){
r = (int)(Math.random()*10000);
arbre.inserer(r);
}
System.out.println("Affichage de l'arbre sous forme de liste triee :");
arbre.afficherArbreListe();
System.out.println("Donnez une cle à rechercher dans le B_arbre :");
n = (new Scanner(System.in)).nextInt();
if( arbre.rechercher(n) == null){
System.out.println("L'entier n'existe pas");
}
else {
System.out.println("L'entier existe");
}
}
}
Catégories
Savoirs les plus récents
-
Création de tableaux en HTML
HTML5 -
PHP DateTime : créez, comparez et formatez des dates
PHP -
Correction algorithme : Généalogie
Algorithmes -
Correction algorithme : Coupe du monde
Algorithmes -
Correction algorithme : Découpage et collage
Algorithmes

